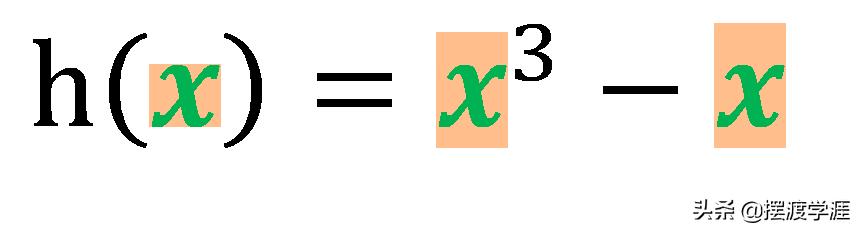奇函数加奇函数是什么函数?怎么证明
奇函数四则运算以后该如何判断函数的奇偶性?
hello,大家好,这里是摆渡学涯,很高兴在这跟大家见面了,马上要进入期中考试了,你的复习准备到哪里了?这次课程咱们来讲一下奇函数相关的变形考点,对于奇函数进行四则运算该如何判断函数的奇偶性呢?

1 已知f(x)为奇函数,判断–f(x)的奇偶性
证明:因为f(x)为奇函数,所以f(x)的定义域关于原点对称,且满足:f(x)=-f(-x),因此-f(x)的定义域关于原点对称,且-f(x)=f(-x),令g(x)=-f(x),则g(x)=-g(-x),即g(x)为奇函数,则-f(x)为奇函数。
下面咱们给出个实际的例子:已知f(x)=x,-f(x)=-x,则-f(x)为奇函数。相关的证明你下去自己证明一下吧。(温馨提示,根据奇函数的定义即可证明出来哦。)

2 已知f(x)是奇函数,判断f(-x)的奇偶性
证明:因为f(x)为奇函数,所以f(x)的定义域关于原点对称,且满足:f(x)=-f(-x),因此-f(x)的定义域关于原点对称,且-f(x)=f(-x),令g(x)=-f(x),则g(x)=-g(-x),即g(x)为奇函数,则-f(x)为奇函数。
下面咱们给出个实际的例子:已知f(x)=x,-f(x)=-x,则-f(x)为奇函数。相关的证明你下去自己证明一下吧。(温馨提示,根据奇函数的定义即可证明出来哦。)
3 已知f(x)和g(x)都是奇函数,且定义域相同,判断f(x)g(x)的奇偶性
证明:因为f(x),g(x)为奇函数,所以f(x),g(x)的定义域关于原点对称,且满足:f(x)=-f(-x),g(x)=-g(-x)因此f(x)g(x)的定义域关于原点对称,且f(x)g(x)=f(-x)g(-x),令h(x)=f(x)g(x),则h(x)=h(-x),即g(x)为偶函数,则f(x)g(x)为偶函数。
下面咱们给出个实际的例子:已知f(x)=x,g(x)=-x,则f(x)g(x)=-x的平方为偶函数。相关的证明你下去自己证明一下吧。

4 已知f(x)和g(x)是表达式不互为相反数奇函数,且定义域相同,判断f(x)+g(x)的奇偶性
证明:因为f(x),g(x)为奇函数,所以f(x),g(x)的定义域关于原点对称,且满足:f(x)=-f(-x),g(x)=-g(-x)因此f(x)+g(x)的定义域关于原点对称,且f(x)+g(x)=-f(-x)-g(-x),令h(x)=f(x)+g(x),则h(x)=-h(-x),即g(x)为奇函数,则f(x)+g(x)为奇函数。注意:当两个函数的表达式互为相反数的时候,此时的函数为常数函数,常数函数的奇偶性我们是不做要求的哦。
下面咱们给出个实际的例子:已知f(x)=x,g(x)=2 x,则f(x)+g(x)=-3 x为奇函数。相关的证明你下去自己证明一下吧。
5 已知f(x)和g(x)是不相等的两个奇函数,且定义域相同,判断f(x)-g(x)的奇偶性
根据4相关的证明即可进行相关的证明哦。证明过程留给你自己去证明了。咱们给出结论f(x)-g(x)没有奇偶性(奇偶性不确定)。例如:f(x)=x的三次方,g(x)=x,f(x)-g(x)非奇非偶哦。完整的证明过程你一定要自己去写一下哦,否则你还是不理解奇函数哦。如果你还是没有证明出来,请跟我们一起交流遇到的困难哦。咱们下次课再见吧。当然你也可以考虑一下函数的除法,自己给出证明的。
时间关系,本次课程我们就为大家分享到这里了,我们下次课再见。如您有相关的疑问,请在下方留言,我们将第一时间给以大家满意的回复。
声明:本文为摆渡学涯的原创文章,未经作者同意不得进行相关的转载和复制,剽窃者是可耻的。翻版必究。
标签:
93
林更新为何被大家称为林狗?原来一夜不睡怼黑粉果然是名不虚传! 近日热播古偶剧《与凤行》里的男主角大家都认识吧?这位传说中的怼黑粉第一人,果然是名不虚传啊[捂脸][捂脸...

179
卡米拉:从弃儿到王后,曾因遭受谩骂在与查尔斯的婚礼上以泪洗面 随着伊丽莎白二世女王离世,卡米拉王后和她的丈夫查尔斯三世国王开始一起承担新的角色。但说实话,在查尔斯的...

55
储能电池介绍(二)钛酸锂电池 技术原理 钛酸锂负极锂离子电池主要由正极材料、电解质、隔膜和负极钛酸锂(Li4Ti5O12)材料组成。锂离子电池正极材料一般由能够可逆脱嵌锂离子的...

132
这是谁画的《八骏图》,笑死我了 (此处已添加圈子卡片,请到今日头条客户端查看) 最近,听说江湖上又惊现了消失已久的 八骏图。 我经不住诱惑,想着,就算倾家荡产,卖车卖房...
89
新时代东北振兴铁路补链工程-沈阳至辽阳至鞍山城际铁路 铁路:规划沈辽鞍城际铁路,辽阳市域一期线规划路串联灯塔、河东、首山,二期规划至小屯、弓长岭。采用“高密度、小编...

145
体操冠军比赛摔成瘫痪,索赔130亿,监护人悉心照顾却被告上法庭 体操冠军比赛中摔成瘫痪,索赔130亿,监护人悉心照顾却被告上法庭。被称为天才运动员的桑兰,职业生涯因为一次意...

57
十大最凶猛的狗,中国藏獒竟然只排第六,排名第一的是它! 10、牛头梗(怪异杀手) 牛头梗3分钟之内就能咬死一头德国黑背,牛头梗的身体很重!有像鲨鱼样的嘴的咬合力,再加上悄...

74
平成骑士天花板,逢魔能力设定详解 在昨天的逢魔时王大结局后,很多人不由得被这帅气的变身特效吸引,毕竟是结局,东映也是花足了钱在逢魔时王的变身特效上,让很多观众爽了一...

81
渔民捕到“天价鱼”:一条价格卖到347万,黄唇鱼为何如此值钱? 大家听说过黄唇鱼吗?它是我国所有鱼类里面,价格可以算得上顶级的一种鱼类。之前在南澳的海域地区有一艘福建的...
94
《怦然心动》高清图片壁纸,谁想和你做朋友?我只想做你男朋友 动动小手指分享关注哦 第一时间 收图抢沙发 哦~ 即使现在和未来遇到更多的人 我们都会是对方最特别的那个。 人与...

124
中央别墅区老牌涉外别墅-裕京花园 裕京花园楼盘简介 裕京花园作为北京最早期高端涉外别墅,原始业主、住户以外籍人士港澳台同胞为主,外国人习惯把工作区和生活区分开,从裕京...

98
一瓶依云矿泉水卖到13元,纪念版700元,它是如何变成奢侈品的? 最近看电视,经常重复播放着一个矿泉水的广告,整个画面是中世纪的欧洲,背景是古老的城堡、石板铺砌的中古街道...

67
张庭主演的电视剧你看过几部? 前段时间偶然看了几集张庭主演的《穿越时空的爱恋》,话说张庭这个名字好像很久没有出现在演艺圈了,但是人们对他的印象却记忆犹新。今天,我们...

160
我的世界:聊聊1.20.2的村民贸易平衡,制图师的“击鼓传花”! 01 击鼓传花! “击鼓传花”是中国古老的一个民间游戏,流行于中国各地。数人、十数人或数十人围成一个圆圈席地而...

118
天下第一御泉—华清宫之杨贵妃的八卦 本文作者:蒹葭 唐华清宫,是唐代封建帝王游幸的别宫。后也称“华清池”,位于陕西省西安市临潼区。 (图片来自好友阿党) 华清宫背山面渭...

108
风水类古本口诀《分金论》...

159
12分钟可达!票价8元!从天河机场“瞬移”到汉口,每日开行车辆…… 视频加载中... 长江日报大武汉客户端3月21日讯(记者徐丹 通讯员宋萍) 很多人不知道,天河机场里还有一座高铁...

93
5个被球迷遗忘的利物浦球员!知道他们的都是老KOP了 利物浦在2021-22赛季有一个很棒的赛季,在上个赛季以微弱优势获得前四名后,克洛普的球队在本赛季卷土重来。 有范迪克在后场,...

192
中苏关系破裂的时间以及原因是什么? 中苏关系破裂的时间是 20世纪60年代 ,导火线是:1958年,中苏之间发生了 “长波电台”和“联合舰队” 事件。中苏关系的破裂的主要原因是:①...

99
一拳超人漫画壁纸大全 收藏必备 一拳超人收集壁纸大全 收藏必备 一拳超人收集壁纸大全 收藏必备 英雄排名S级第2位 龙卷 一拳超人收集壁纸大全 收藏必备 一拳超人收集壁纸大全 收藏...