零点定理的一个拓扑学证明
我们高中时都学过一个非常常用的定理,零点定理,或者也叫介值定理(弱化版)。它的内容叙述如下:
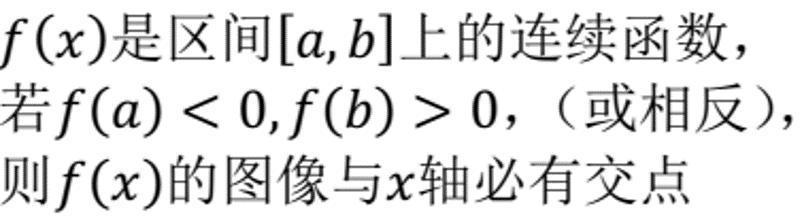
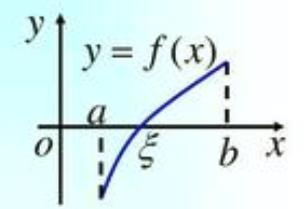
它的图形画出来如下所示
这个定理表面上看起来非常显然,似乎不需要证明。但事实上,数学上任何一个定理,即使看起来再显然,也是需要经过严格证明的。我之前曾写过一篇文章介绍过零点定理的证明,使用的是数学分析中的确界原理。文章链接如下:
一个看似极其显然,证明却极其困难的数学定理
确界原理是实数完备性定理中的一个重要定理,与此同时还有另外五个与之等价的定理,一共六个定理,数学专业的同学会在《数学分析》这门课程里面学的,这六个定理都可以用来证明零点定理,因此我在文章中说,它的证明方法一共有六种。后来有网友评论到,其实可以跳出实数完备性定理的框架,用更高级的数学知识,比如拓扑学来证明。于是我在其启发下,想到了一种用拓扑学的知识来证明该定理的方法,本文就来介绍,欢迎讨论。

当然既然要利用拓扑学的知识,就首先对拓扑学的一些基本概念做一些简要介绍。拓扑学的研究对象非常复杂,但仅就零点定理而言,我们只需要理解一维实数轴上的拓扑空间就足够了,我将用最简单的语言来进行描述。
概念1:开集
设U为实数集的一个子集,如果U满足如下条件:
从U中任取一个数a,都可以找到一个以a为中心的小的开区间(a-δ,a+δ),使得这个小区间完全包含在U里面。
那么就称U为一个开集。
任何一个开区间都是开集,比如我们拿(0,1)举例子。我在上面任意选一个数,比如0.5,那么(0.4,0.6)是完全包含在(0,1)之间的。选的数离1很近也不要紧,比如0.99,那么(0.989,0.991)是完全包含在(0,1)里的,诸如此类,所以开区间(0,1)就是一个开集。
当然开集不只是包含开区间,任意两个开区间的并集也是开集,比如(0,1)∪(2,3)。
同时,有界闭区间就不是开集了,比如闭区间[0,1]。因为我可以在上面取一个点1,任何一个以1为中心的小的开区间都不能完全包含在[0,1]之内。所以有界闭区间不是开集。
那么闭区间到底是一个什么样的集合呢?这时我们就需要引入闭集的概念。
概念2:闭集
设V为实数集的一个子集,如果它的补集是一个开集,那么称V为一个闭集。
于是很显然,一个有界闭区间就是一个闭集。我们还拿[0,1]举例子,它的补集(-∞,0)∪(1,+∞)是一个开集,因此它是一个闭集。同样道理,两个闭区间的并集也是闭集。
从上面对开集的定义中,我们可以很明显地看出如下定理:
定理:多个开集的并集还是开集
但凡定理都需要证明,这个定理的证明比较容易,我们就拿两个集合举例。假设集合A与集合B都是开集,下面我们来研究A∪B。从A∪B中任取一个元素x,那么x至少在A或B中的一个里面。如果x在A里面,那么因为A是开集,根据开集的定义,我们就可以找到一个以x为中心的小区间(x-δ,x+δ),使得它完全包含在A里面,A肯定完全包含在A∪B里面,所以(x-δ,x+δ)一定完全包含在A∪B里面。同样道理,如果x在B里面,我们也可以类似证明。所以对于你任意取的一个x,一定可以找到以x为中心的小区间完全包含在A∪B里面,于是A∪B就是一个开集。
开集和闭集是拓扑学中最基本的两个概念,他们在一般的拓扑空间中有着更抽象的定义,但是本文涉及不到。本文介绍的只是在一维实数轴上所对应的开集与闭集的定义,用它我们就可以来证明零点定理了。

我们把问题再具体叙述一下。
f(x)在[a,b]上连续,且f(a)<0,f(b)>0,求证在该区间内必存在一点使得f(x)=0
证明:我们把闭区间[a,b]中所有的数分为三个集合,分别用A,B,C表示:
A = { x∈[a,b] | f(x)<0 }
B = { x∈[a,b] | f(x)>0 }
C = { x∈[a,b] | f(x)=0 }
一个数无非小于0,大于0,等于0三种情况,于是 A∪B∪C = [a,b]。
我们来证明C一定不是空集。这样一来C中至少包含一个元素,这些元素就是f(x)=0的点。
采用反证法:假设C是空集。
于是就只剩下A和B,即 A∪B =[a,b]。
对于集合A,随便选一个点c∈A,则有f(c)>0,因为函数连续,则

现在已知f(c)>0,因此利用函数极限的保号性,存在某个小区间(c-δ,c+δ),使得x∈(c-δ,c+δ)时有f(x)>0,也就是这个小区间内所有的数都在满足集合A的条件,也就是说它都在A里面,即(c-δ,c+δ)⊂A,那么根据上面开题的定义,因为这个c是任意选的,所以A一定是一个开集。
同理,利用极限的保号性可以证明集合B也一定是一个开集。
按照我们前面讲过的定理:两个开集的并集也是开集,于是A∪B 也是开集,又因为我们前面按照假设A∪B =[a,b],因此[a,b]也是开集。
但我们前面经过论证,有界闭区间一定不是开集,于是得到矛盾,假设不成立,即C不是空集。
于是C中包含的数就是使f(x)=0的数,证毕。
用这种方法来证明零点定理,过程相对比较简单,但是理解起来相对困难,因为它使用了拓扑学中开集这个概念。而开集又是依赖于开区间的,这道题的关键是利用极限的保号性构造出一个小的开区间,把这块儿理解了,那么整个过程也就不难理解了。
零点定理在证明方程解的存在性等问题中有着决定性的作用,同时还可以利用它进行方程的求解,比如说二分法,就是利用的零点定理来数值求解方程。
当然,证明零点定理不是只有这一种方法,即使是在拓扑学的框架内,相信也有很多同学能想出其他的方法来。如果有同学有新的方法,可以在评论中提出,欢迎热爱数学的小伙伴们一起来加入讨论!